Standard Error Calculator

You can use the Standard Error Calculator in order to derive the standard error of the mean. Example is included below.

Enter Values (each value separated by a comma):

How to Use the Standard Error Calculator

Let's review a simple example in order to demonstrate how to use the calculator.

To start, suppose that you have the following values, and you'd like to derive the standard error of the mean:

5, 9, 14, 3, 7

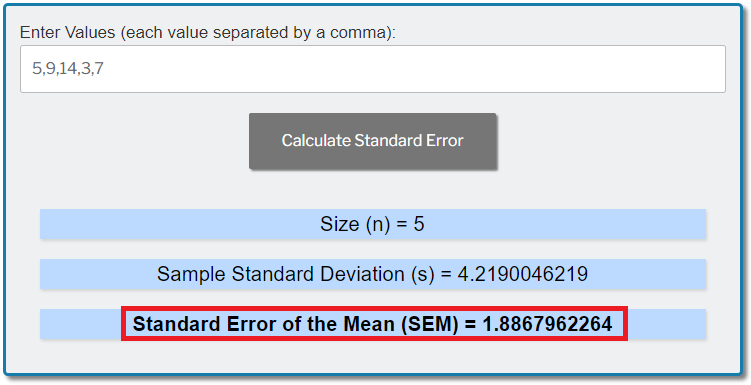
Enter the values in the calculator, and then click on the 'Calculate Standard Error' button:

Standard Error Calculator

You'll then get the SEM of 1.886796:

Standard error of the mean

How to Manually Calculate the Standard Error

You can use the following formula to calculate the standard error of the mean:

                                                                        s    
Standard Error of the Mean (SEM)  =     (n)0.5   

Where:

  • SEM = Standard Error of the Mean
  • s = Sample Standard Deviation
  • n = Sample size

For example, let's calculate the standard error of the mean, given the values below:

5, 9, 14, 3, 7

First, calculate the sample standard deviation (s) using:

  • x̅ = Sample Mean (average of all data points) = (5+9+14+3+7) / 5 = 7.6
  • Σ(xi - x̅)2 = (5-7.6)2 + (9-7.6)2 + (14-7.6)2 + (3-7.6)2 + (7-7.6)2 = 71.2
  • n = 5
                                                             [ Σ(xi - x̅)2 ]0.5     [71.2]0.5
Sample Standard Deviation (s)  =      (n-1)0.5    =      (5-1)0.5  =  4.219005

You'll then get the sample standard deviation of 4.219005.

Next, calculate the standard error of the mean (SEM) using:

                                                                         s           4.219005 
Standard Error of the Mean (SEM)  =     (n)0.5  =      (5)0.5    = 1.886796

You'll now get the SEM of 1.886796.