The Standard Deviation Calculator can be used to calculate both the Population Standard Deviation, as well as the Sample Standard Deviation. Each value should be separated by a comma. Example is included below.
How to use the Standard Deviation Calculator
Let's review a simple example to demonstrate how to use the Standard Deviation Calculator, where:
- The data points to be entered into the calculator are: 2,7,15,4,8
To get the Standard Deviation, simply type/copy the above data points into the entry box, and then click on the Calculate Standard Deviation button:
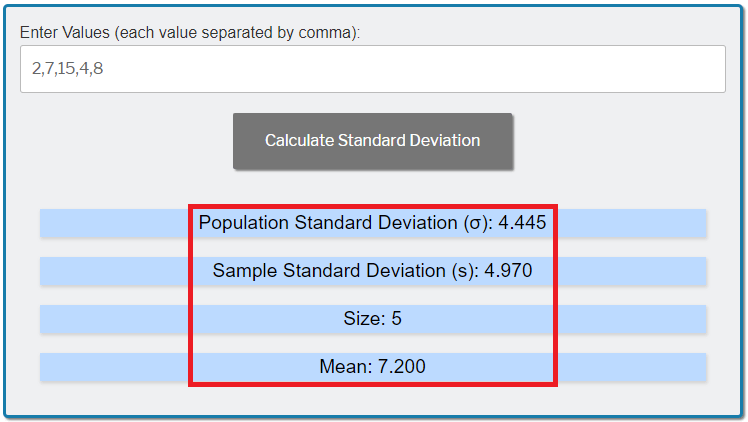
You'll then get the the Population Standard Deviation of 4.445, and the Sample Standard Deviation of 4.970:
How to Manually Calculate the Standard Deviation
You can use the following formula to calculate the Population Standard Deviation:
[Σ(xi - μ)2]0.5
Population Standard Deviation (σ) = (N)0.5
Where:
- μ = Mean (average of all data points)
- xi = Value of each data point
- N = Total number of data points
Alternatively, you may use this formula to get the Sample Standard Deviation:
[ Σ(xi - x̅)2 ]0.5
Sample Standard Deviation (s) = (n-1)0.5
Where:
- x̅ = Sample Mean (average of all data points)
- xi = Value of each data point
- n = Sample size
Calculation Example
Suppose that you have the following data points: 2,7,15,4,8.
Your goal is to calculate the:
- Population Standard Deviation (σ); and
- Sample Standard Deviation (s)
Calculate the Population Standard Deviation
- μ = (2+7+15+4+8) / 5 = 7.2
- Σ(xi - μ)2 = (2-7.2)2 + (7-7.2)2 + (15-7.2)2 + (4-7.2)2 + (8-7.2)2 = 98.8
- N = 5
[Σ(xi - μ)2]0.5 [98.8]0.5 Population Standard Deviation (σ) = (n)0.5 = (5)0.5 = 4.445
You'll then get the Population Standard Deviation of 4.445.
Calculate the Sample Standard Deviation
- x̅ = (2+7+15+4+8) / 5 = 7.2
- Σ(xi - x̅)2 = (2-7.2)2 + (7-7.2)2 + (15-7.2)2 + (4-7.2)2 + (8-7.2)2 = 98.8
- n = 5
[ Σ(xi - x̅)2 ]0.5 [98.8]0.5 Sample Standard Deviation (s) = (n-1)0.5 = (5-1)0.5 = 4.970
You'll now get the Sample Standard Deviation of 4.970.