Bond Duration Calculator – Exploring Finance

The Bond Duration Calculator can be used to derive the duration of a bond:

Number of Years to Maturity: Yield or Market Rate (%): Bond Face Value: Annual Coupon Rate (%): Annually
Semiannually
Quarterly
Monthly

Example of using the Bond Duration Calculator

Suppose that you have a bond, where the:

Number of years to maturity is 2
Yield is 8%
Bond face value is 1000
Annual coupon rate is 6%
Payments are semiannual

(1) What is the bond’s Macaulay Duration?
(2) What is the bond’s Modified Duration?

You can easily calculate the bond duration using the Bond Duration Calculator. Simply enter the following values in the calculator:

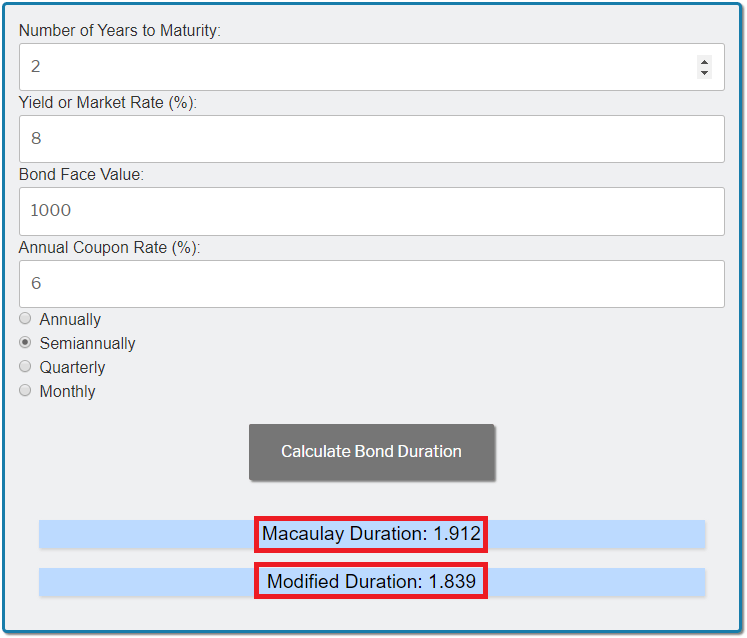
Once you are done entering the values, click on the 'Calculate Bond Duration' button and you'll get the Macaulay Duration of 1.912 and the Modified Duration of 1.839:

Formulas to Calculate the Bond Duration

You can use the following formula to calculate the Macaulay Duration (MacD):

                        (t1*FV)(C)                                  (tn*FV)(C)                           (tn*FV)   
MacD = (m*PV)(1+YTM/m)^mt₁  + ... + (m*PV)(1+YTM/m)^mt_n  + (PV)(1+YTM/m)^mt_n

Where:

m = Number of payments per period
YTM = Yield to Maturity
PV = Bond price
FV = Bond face value
C = Coupon rate
t_i = Time in years associated with each coupon payment

For example, let's suppose that you have a bond, where the:

Number of years to maturity is 2
Yield is 8%
Bond face value is 1000
Annual coupon rate is 6%
Payments are semiannual
Bond price is 963.7

Based on the above information, here are all the components needed in order to calculate the Macaulay Duration:

m = Number of payments per period = 2
YTM = Yield to Maturity = 8% or 0.08
PV = Bond price = 963.7
FV = Bond face value = 1000
C = Coupon rate = 6% or 0.06

Additionally, since the bond matures in 2 years, then for a semiannual bond, you'll have a total of 4 coupon payments (one payment every 6 months), such that:

t₁= 0.5 years
t₂= 1 years
t₃= 1.5 years
t₄=t_n= 2 years

Pay special attention to the last period (t₄=t_n= 2 years) which requires both the coupon payment as well as the final principal repayment.

Let's now plug all those components within the MacD formula:

                  (0.5*1000)(0.06)                    (1*1000)(0.06)                   (1.5*1000)(0.06)                  (2*1000)(0.06)                      (2*1000)      
MacD = (2*963.7)(1+0.08/2)^2*0.5  + (2*963.7)(1+0.08/2)^2*1 + (2*963.7)(1+0.08/2)^2*1.5 + (2*963.7)(1+0.08/2)^2*2 + (963.7)(1+0.08/2)^2*2

MacD = 0.01496 + 0.02878 + 0.04151 + 0.05322 + 1.7740 = 1.912

Once you calculated the Macaulay duration, you'll be able to use the formula below in order to derive the Modified Duration (ModD):

                      MacD   
ModD =  (1+YTM/m)

For our example:

                     1.9124   
ModD =  (1+0.08/2)

The Modified duration is therefore = 1.839

You may refer to the following guide that further explains how to calculate the Bond Duration.