Please enter your values in the Capital Asset Pricing Model (CAPM) Calculator. Example is included below.
How to use the Capital Asset Pricing Model (CAPM) Calculator
Let’s now review a simple example to demonstrate how to use the CAPM calculator.
To start, let’s suppose that you’d like to derive the Expected Return of a security, given the following information:
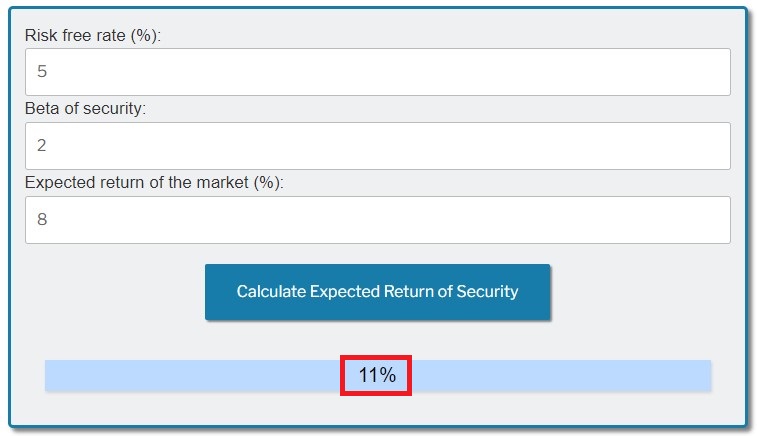
- The Risk Free Rate is 5%
- The Beta of the security is 2
- The Expected Return of the Market is 8%
Based on the above information, enter the values in the CAPM Calculator to get the Expected Return of the security:

Once you entered the values in the calculator, click on the “Calculate Expected Return of Security” button, and you’ll get the expected return of 11%:
How to Manually Derive the Expected Return of a Security
You can also derive the Expected Return of a security using the formula below:
E(Ri) = Rf + βi[E(Rm) – Rf]
Where:
- E(Ri) = expected return of security i
- Rf = risk free rate
- βi = beta of security i
- E(Rm) = expected return of the market
To demonstrate how to apply the formula in practice, let’s review an example, where the goal is to derive the Expected Return of a security, given the following information:
- The Risk Free Rate is 5%
- The Beta of the security is 2
- The Expected Return of the Market is 8%
In that case, the Expected Return of the security is 11%:
E(Ri) = Rf + βi[E(Rm) – Rf] = 5% + 2[8% - 5%] = 11%