The following Covariance Calculator can be used to derive both the Population Covariance as well as the Sample Covariance. Each value entered in the calculator should be separated by a comma. Example is included below.
How to use the Covariance Calculator
Let's review a simple example to see how to use the Covariance Calculator in practice.
Suppose that your goal is to derive the Covariance, given the following data:
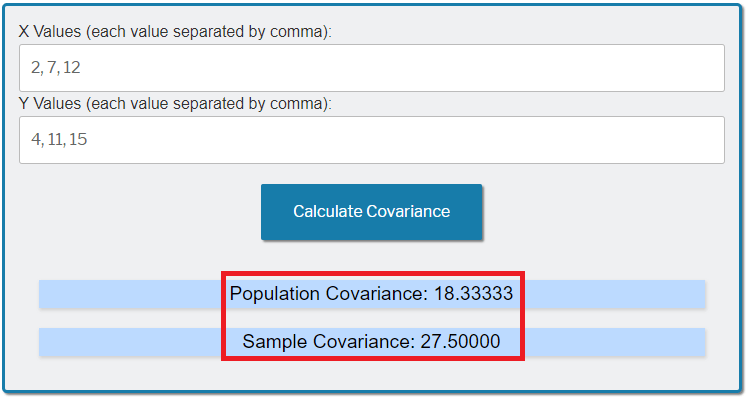
- The X values are: 2, 7, 12
- The Y values are: 4, 11, 15
To start, enter the above values in the calculator, and then click on the Calculate Covariance button:

You'll then get the Population Covariance of 18.33, and the Sample Covariance of 27.50:
How to manually derive the Covariance
You may use the following formula to get the Population Covariance:
Σ [(xi - x̅) * (yi - ȳ)]
Population Covariance = n
Alternatively, you may use the formula below to derive the Sample Covariance:
Σ [(xi - x̅) * (yi - ȳ)]
Sample Covariance = n - 1
For example, let's say that your goal is to derive the Population and Sample Covariances, given the following data:
- The X values are: 2, 7, 12
- The Y values are: 4, 11, 15
To start, calculate the averages:
2 + 7 + 12
Average ( x̅ ) = 3 = 7
4 + 11 + 15
Average ( ȳ ) = 3 = 10
Next, calculate the Population Covariance :
[(2 - 7) * (4 - 10)] + [(7 - 7) * (11 - 10)] + [(12 - 7) * (15 - 10)]
3 = 18.33
You'll then get the Population Covariance of 18.33.
Finally, calculate the Sample Covariance:
[(2 - 7) * (4 - 10)] + [(7 - 7) * (11 - 10)] + [(12 - 7) * (15 - 10)]
3 - 1 = 27.50
You'll now get the Sample Covariance of 27.50.